1228. Add All
The cost of
adding two numbers is equal to their sum. For example, to add 10 to 1, you need
to pay 11. The task requires adding all the given numbers in a way that
minimizes the total cost.
For example,
adding the numbers 1, 2, and 3 can be done in three ways:
·
1 + 2 = 3 (cost
= 3), 3 + 3 = 6 (cost = 6), Total
= 9
·
1 + 3 = 4 (cost
= 4), 2 + 4 = 6 (cost = 6), Total
= 10
·
2 + 3 = 5 (cost
= 5), 1 + 5 = 6 (cost = 6), Total
= 11
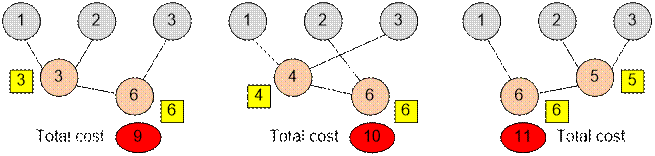
The first way of adding is
the cheapest.
Input. The first line contains a positive integer n (2 ≤ n
≤ 105). The second line contains n nonnegative integers, each not exceeding 105.
Output. Print the
minimum cost of adding all the numbers.
|
Sample
input |
Sample
output |
|
4 1 2 3 4 |
19 |
SOLUTION
greedy
Algorithm analysis
Each
time, two smallest numbers should be added together. This way, the total cost
of adding all n integers will be minimized. Since numbers can repeat, it is
convenient to store them in a multiset.
Example
To minimize the
cost of addition, add the numbers in the following order:
1. Add 1 and 2 to get 3. Cost of addition is 3.
2. Add 3 and 3 to get 6. Cost of addition is 6.
3. Add 4 and 6 to get 10. Cost of addition is 10.
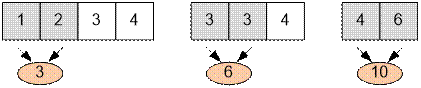
The total cost of addition
is
3 + 6 + 10 = 19.
Algorithm implementation
The input numbers are
stored in a multiset s (numbers can repeat). The two smallest numbers
are always located at the beginning of the multiset.
multiset<long
long> s;
Read the number of
elements n.
scanf("%lld",&n);
Read the sequence of numbers
and add them to the multiset s.
for (i = 0; i <
n; i++)
{
scanf("%lld",&x);
s.insert(x);
}
The total cost of adding
all numbers is computed in the variable res.
res = 0;
While there is more than
one number in the multiset s, extract and add the two smallest elements,
then add their sum back into s. The cost of adding numbers a and b
is a + b, and this cost is added
to res.
while (s.size() >
1)
{
a = *s.begin(); s.erase(s.begin());
b = *s.begin(); s.erase(s.begin());
s.insert(a + b);
res += a + b;
}
When only one number
remains in the multiset, print the answer – the value of the variable res.
printf("%lld\n",res);
Algorithm implementation –
priority queue
Declare a priority queue pq, where the smallest element is always
at the front.
priority_queue<long long, vector<long long>,
greater<long long>
> pq;
Read the number of
elements n.
scanf("%lld",&n);
Read the sequence of numbers
and add them to the priority queue pq.
scanf("%lld",&n);
for (i = 0; i <
n; i++)
{
scanf("%lld",&x);
pq.push(x);
}
The total cost of adding
all numbers is computed in the variable res.
res = 0;
While there is more than
one number in the priority queue pq, extract
and add the two smallest elements, then add their sum back into pq. The cost of adding numbers a
and b is a + b, and this cost is added to res.
while (pq.size() >
1)
{
a = pq.top(); pq.pop();
b = pq.top(); pq.pop();
pq.push(a + b);
res += a + b;
}
When only one number
remains in the priority queue, print the answer – the value of the variable res.
printf("%lld\n",res);
Java implementation
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
PriorityQueue<Long> pq = new PriorityQueue<Long>();
for(int i = 0; i < n; i++)
{
long val = con.nextLong();
pq.add(new Long(val));
}
long Result = 0;
while(pq.size() > 1)
{
long a = pq.poll();
long b = pq.poll();
pq.add(a + b);
Result += a + b;
}
System.out.println(Result);
}
}
Python implementation
Declare a priority queue q, where the smallest element is always at
the front.
from queue import PriorityQueue
q = PriorityQueue()
Read the input data.
n = int(input())
lst = map(int,input().split())
Add the numbers to the
queue q.
for x in lst:
q.put(x)
The total cost of adding
all numbers is computed in the variable res.
res = 0
While there is more than
one number in the priority queue q, extract
and add the two smallest elements, then add their sum back into q. The cost of adding numbers a
and b is a + b, and this cost is added to res.
while q.qsize() > 1:
a = q.get()
b = q.get()
q.put(a + b)
res += a + b
When only one number
remains in the priority queue, print the answer – the value of the variable res.
print(res)